Strategies For Creating Efficient, Beautiful Whites

There is much to like about solid-state lighting: It trims global energy consumption, opens new lighting applications, and gives us a long-lasting light bulb that hits full brightness in an instant. However, penetration of this technology is not as fast as we would like, with adoption held back by high prices and an insufficient level of superiority over incumbent sources.
Many of the LED bulbs that are on sale today have at their heart a blue-emitting chip coated with one of more phosphors emitting at longer wavelengths. White light stems from colour-mixing, which can also be produced by combining either the output of blue, green and red LEDs; or the emission of a quartet of blue, green, amber and red devices. Whichever approach is taken, the designers of white-light sources have to make two key decisions: how many, and what kind of individual emitters should be chosen to produce white light with desired properties; and what are the requirements for characteristics of the individual emitters. Getting the right answers demands careful optimization of light mixing, because it is not just a matter of optimizing the total emission spectrum produced by all the emitters "“ it also requires maximising the efficiency of electricity-to-light conversion of each individual device.
LEDs and phosphors
Today's solid-state white light sources are based on III-nitride (III-N) LEDs, possibly combined with III-phosphide (III-P) cousins. Both of these forms of LED have a width and shape of the spectral emission that is normally asymmetric relatively to the peak wavelength (see Figure 1a and 1b), and one of their key figures of merit is the wall-plug efficiency, which is the efficiency of electricity-to-light conversion. This efficiency depends on the current passing through the chip, and when it peaks, it is almost equal to the external quantum efficiency (essentially, this is the proportion of photons emitted for every electron and hole injected into the device).
Plotting the external quantum efficiency for a range of LEDs emitting at different wavelengths highlights a problem known as the "˜green gap' (see Figure 1(c), which is based on the performance of a range of leading commercial LEDs from various chipmakers). The "˜green gap' results from a lack of efficient LEDs emitting at 500-600 nm for reasons that are not yet completely understood, despite the practical importance of this issue.
Since the wall-plug efficiency of the LED varies with wavelength, calculations of the efficiency of a white-light source constructed from a collection of emitters of different colours requires a summing of individual contributions, and determining what the average of these is. Armed with this information, it is then possible to calculate the efficacy of the light source: It is the product of the wall-plug efficiency and a characteristic known as the luminous efficacy of radiation, which accounts for the spectral response of the human eye (see the panel "White light and its characteristics" for more details). Note that it is also possible to determine the efficiency of the light source when phosphors are used. To do this requires the inclusion of terms in the calculation that reflect the energy loss associated with the differences in excitation and emission wavelengths, and the quantum yield of the phosphor emission.
Whether phosphors are used or not, the aim of colour-mixing is to maximise the performance of the white-light source via judicious selection of the number of individual light emitters, their emission wavelengths, and the fraction of power that they contribute to the total emission spectrum. For specific lighting applications, the characteristic that is most frequently considered is the correlated colour temperature: For a warmer white, this value is lower; but if a harsher, more revealing white is preferred, a higher value is needed.
There are also other measures that reflect the quality of the light: The higher the colour rendering index, the better the colour rendition; the higher the luminous efficacy of radiation, the higher the total emission spectrum and the luminous flux; and the higher the efficacy of the light source, the brighter it is.
The easiest, most frequently applied approach to building a better light source is to optimise simultaneously the colour-rendering index and the luminous efficiency of radiation. However, this approach only considers the emission spectrum of the light source, and it ignores the efficiencies of individual emitters. What's more, this approach is non-trivial, because it is not possible to independently optimise the colour-rendering index and the luminous efficiency of radiation, as they have to be traded against one another (see Figure 2). Due to this, the best result depends on the task facing the light source. If, for example, it is to be used to illuminate paintings, excellent colour rendition is the primary objective.
A different situation arises when the efficiencies of individual light emitters are taken into account. At the STR Group of St.Petersburg, Russia, we have taken this approach and discovered that the spectral dependencies of the emitter wall plug efficiencies have a crucial impact on the optimization results, making the choice of the white-light characteristics more evident and clear.
When optimising the colour mixing of a white-light source made from LEDs emitting at different wavelengths, it is critical to account for individual efficiencies and use realistic emission spectra. We have done this, taking values from commercial LEDs, and our calculations have uncovered a distinct transition from optimal three- to four-LED operation at a colour-rendering index of about 92. However, even with three optimal LEDs, it is possible to hit a light source efficacy of 165-170 lm/W and a colour-rendering index of 87-91 at a colour-correlated temperature of 3000 K. Switching to four LEDs can lead to even higher values for the colour-rendering index, but the light source efficacy starts to drop off a cliff (see Figure 3 (b)). That's because the optimal wavelengths of two of the LEDs have to lie within the "˜green gap', and this drags down the efficacy of the white-light source.
An important finding in our theoretical study is that the optimized LED peak wavelength shows only a very weak dependence on a particular colour-correlated temperature (Figure 3 (a)). This implies that a "˜smart' white-light source can be constructed that offers an adjustable colour-correlated temperature, which is selected by tuning the emission intensities of individual LEDs. For example, a combination of a 455 nm, a 532 nm and a 614 nm LED would allow the colour-correlated temperature to be varied from 2700 K to 8000 K while keeping the colour rendering index and the efficacy of the light source relatively stable (they range between 89-91 and 145-170 lm/W).
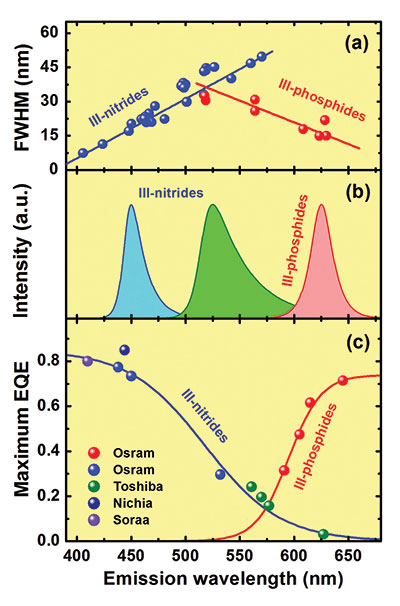
Figure 1: Calculations have considered commercial III-N and III-P LEDs, including values for: emission spectra (a), typical spectrum shapes (b), and maximum external quantum efficiency (EQE) (c). Note that the spectral width of III-N LEDs is greater for devices emitting at a longer wavelength.
"¦ or with phosphors
One common approach for sidestepping problems associated with the green gap is to use a phosphor emitting in the green-yellow. The wall-plug efficiency of the resulting chip can be higher than that of a direct green emitter "“ our calculations suggest that the pairing of a blue-emitting chip and a yellow YAG:Ce3+phosphor, which has a wide emission spectrum peaked at 570 nm, can spawn a device with a wall-plug efficiency of 55 percent. This is a few times higher than LEDs emitting in the green, and it allows the creation of a very high efficacy white-light sources based on two or three LEDs and a phosphor. However, compared to an LED-only approach, optimal wavelengths are generally dependent on the colour-correlated temperature (see Figures 4((a)) and 5 ((a)).
The combination of a nitride LED, a phosphide LED and a YAG phosphor can yield a warm source with an efficacy of 195-200 lm/W, a colour-rendering index exceeding 90, and a colour-correlated temperature of 2400-3000 K (see Figure 4(b)) "“ and even higher temperatures can be realised at the expense of efficacy. This kind of approach known as Brilliant Mix has already been adopted by Osram Opto Semiconductors, which in 2011 launched LEDs that produced an efficacy of 110 lm/W at a colour-rendering index of 90 under practical operation conditions.
We have found that turning from one nitride LED to two of them, while maintaining the phosphide LED and the phosphor, allows the fabrication of promising neutral white light sources with a colour-correlated temperature of 4000 K (see Figure 5 (b)). In this case, an efficacy of 185 lm/W is possible at an extremely high colour-rendering index of 96-98. Such high values can be realised because the optimal peak wavelengths of LEDs do not occupy the "˜green gap'.
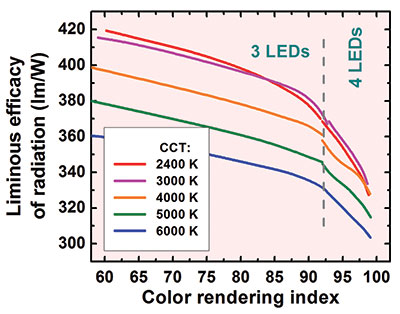
Figure 2: There is a trade-off between the maximum colour rendering index and luminous efficacy of radiation when optimizing the colour mixing in a white-light source comprising of two or three III-N and one III-P LEDs.
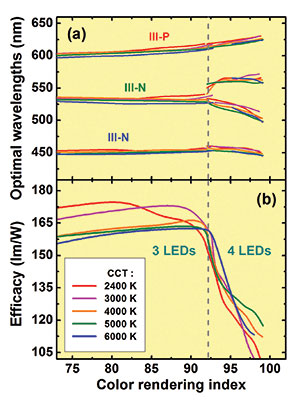
Figure 3: Optimal peak wavelengths of III-N and III-P LEDs (a) and maximum efficacy (b) for different colour rendering indexes of white-light sources comprising of LEDs only.
To drive the development of white light sources that deliver a level of performance in this ballpark, the European Union has funded a Framework 7 programme NEWLED: Nanostructured Efficient White LEDs. This four year effort, which kicked off in late 2012 and is backed by € 11.8 million, is targeting the rather ambitious goal of white-light sources that combine an efficacy of 200 lm/W with a colour-rendering index in excess of 90.
Our calculations, which have been conducted within this project, offer routes to realising this goal. However, does this mean that the optimal ways for colour mixing are now determined, and there is no need for further refinement?
Well, yes and no "“ with the former answer reflecting the situation today, and the latter highlighting the need for further calculations to underpin longer-term efforts. It is worth noting that the results presented here draw on the performance for state-of-the-art LEDs and phosphors, and if improvements were made, particularly in relation to the green gap, the optimal approach for colour mixing would change.
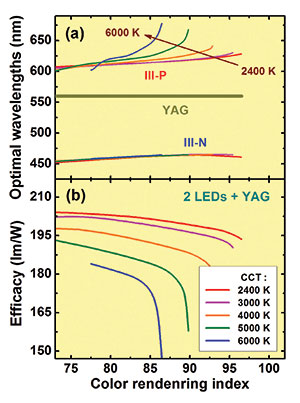
Figure 4: Optimal peak wavelengths of III-N and III-P LEDs (a) and maximum efficacy (b) for different colour rendering indexes of white-light sources comprising of two LEDs and a YAG:Ce3+ phosphor.
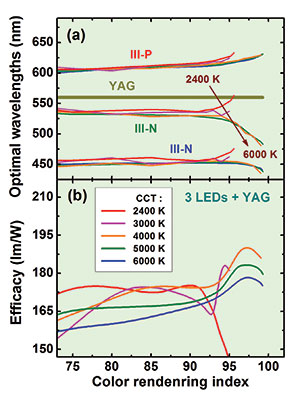
Figure 5: Optimal peak wavelengths of III-N and III-P LEDs (a) and maximum efficacy (b) for different colour rendering indexes of white-light sources comprising of three LEDs and a YAG:Ce3+ phosphor.
We should also point out that our calculations are there to provide a benchmark, because they employ performance figures at drive currents too low for use in solid-state lighting. Given this, it would be both desirable and helpful to carry out calculations that indicate how to optimize colour mixing for LEDs at practical operating currents. On top of this, we would like to extend our study to include the stability of white light characteristics under variations of temperature and the total luminous flux of the light source. Such efforts might give additional insights into how to optimise colour mixing.
Even now, without these refinements, our insights into optimising colour mixing provide guidelines for how to develop high-performance white-light sources. And as more of these sources hit the markets, this will accelerate a lighting revolution.
Further Reading
CIE. Publ. No 15.2, "Colorimetry. Official Recommendations of the International Commission on Illumination", Sec. Ed., Vienna, Central Bureau of the CIE (1986).
K. A. Bulashevich et. al. Phys. Stat. Solidi A (2014) // DOI 10.1002/pssa.201431576.
A. Žukauskas et al. Appl. Phys. Lett. 80 (2014) 234.
http://www.newled-fp7.eu/White light and its characteristics
A wide variety of spectra can form a light source that appears white to the human eye. To account for these differences, the nineteenth century physicist James Clarke Maxwell pioneered the use of three components to describe light, an approach that has subsequently been pursued by the International Commission on Illumination (see Figure 1).
One source of white light is a black body heated up to several thousand Kelvin. As this temperature varies, the chromatic coordinates shift, with a plot of chromatic co-ordinates at different temperatures tracing out a locus that nearly corresponds to white light (see Figure 1).
In practice, small deviations from this locus still produce light that appears white; and projections of the co-ordinates of these points onto the blackbody locus can provide a correlated colour temperature, which is one of the most important characteristics of white light.
Another important characteristic is the luminous efficacy of radiation, a measure that considers the sensitivity of the human eye (see Figure 2). This metric is equal to the total luminous flux measured in lumens and produced by a light source with a given spectrum and a total optical power of 1W.
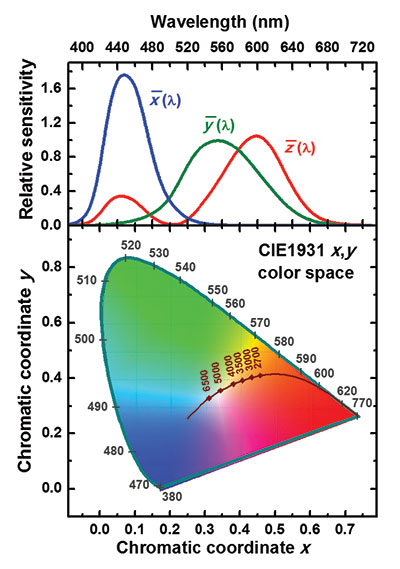
Figure 1: Three colour coordinates X, Y, and Z, can be brought in by convolution of a light source emission spectrum S(λ) with three color matching functions, x(λ) , y(λ), and z(λ). Then the relative chromatic coordinates x=X/(X+Y+Z) and y=Y/(X+Y+Z) project the emission spectrum into the CIE1931 colour chart, represented by points in the (x,y) space. In this chart there are all the possible colours that can be met in practice. Note that the black-body radiation locus (dark-brown line) and points (diamonds) correspond to selected colour temperatures, and the (x,y)-colour space is confined by the pure-colour locus (dark-cyan line) with corresponding wavelengths indicated in nanometres.
Meanwhile, the colour-rendering index reveals the capability of a light source to reproduce properly the colours of illuminated objects. This index accounts for the differences between the chromatic coordinates of light reflected from a number of standard colour samples at their illuminating by the light source studied and by one or another standard illuminant.
The maximum value for the colour-rendering index is 100, and it drops by one for every chromatic coordinate difference obtained from the selected colour samples.
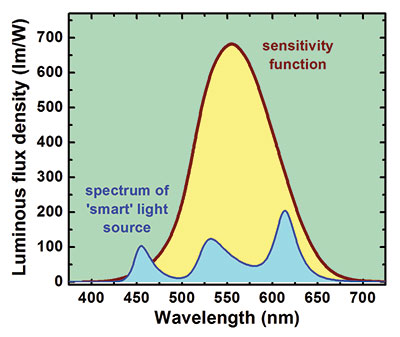
Figure 2: A sensitivity function for the human eye allows the calculation of luminous flux from a light source with a known spectrum and total spectrum of a "˜smart' white-light source operating at a colour-correlate temperature of 3500 K.